早くも一月終わった。
またまたまたまたコロナウイルス関連のニュースが多くなっているが、
街中の雰囲気は特段変わっていない。
観光地は残念ながら客足が遠のいてしまった。
子供の感染が従来より増えているので、家庭内感染も増えてくる。
1月末~2月初めに山を越える(ピークアウト)という予測。
実効再生産数を見ていれば感染者数の増減具合が分かる。
※ uub.jp/cvd/cvd5w.htmlなど
1月初めは各都道府県5とか4が多かったが、
今は2から1が多いので、明らかに増加曲線の傾きは緩くなっている。
1を下回れば減少に転じ、持続すればピークアウト。
最初に増え始めた沖縄は既に1未満。持続中。
もう1点気になる点は、変な変異株が混ざっていないか。
あいにく感染力のより高いオミクロン株亜種 BA.2(B.1.1.529.2)が「ステルス・オミクロン」と呼ばれて取り上げられている。
感染者数がなかなか減らず高止まりのまま、という可能性もある。
※ デンマークがこのBA.2で急増。ただ、深刻な状況に陥っているというわけでもなさそう
昨秋のようにほぼ収まった状態になるのは2月か3月か---。
給付金のタイミング、対象ともに悪かった。
感染症シミュレーション SIRモデル
新型コロナウイルスの流行が始まってから当ブログも20以上記事にしているが、感染症シミュレーションについては触れていなかった。というか結果だけ見させてもらって中身は避けてきた。
一応流行初期(2020年)にSIRモデル(ケルマック-マッケンドリックモデル)という感染症数理モデルを理解しようと試みたので、
今回の一番の「大波」(流行末期であると思いたい)を機に少しまとめておいた。
SIRモデルとは……要約すると、
集団を
Susceptible --- 未感染者
Infected --- 感染者
Recovered --- 回復者および死者
の3つに分けて各々の変化を捉える数理モデル。
順番にS⇒I⇒Rの経過を辿り、
各々の時間変化が
・ dS(t)/dt = -βS(t)I(t)
・ dI(t)/dt = βS(t)I(t) - γI(t)
・ dR(t)/dt = γI(t)
β:感染率
γ:回復率
で表されるモデル。
数式は微分方程式。
(今回は説明パス)。
ひとまず
dS(t)/dt = {S(t+dt)-S(t)}/dt、dI(t)/dt = ……
※ 分母は(t+dt)-t
と置き換えて上の3つの時間変化の式を全て足すと
S(t+dt)+I(t+dt)+R(t+dt) = S(t)+I(t)+R(t)
になる。
どの時点においても皆S、I、Rのいずれかに属する。
S+I+R=一定の値=N(総人口)。
※ 人口動態は考慮しない
コンピューターに計算させれば、曲線を描いてくれるので、こちらから入門したほうが理解が進むかもしれない---
ということで、
R言語
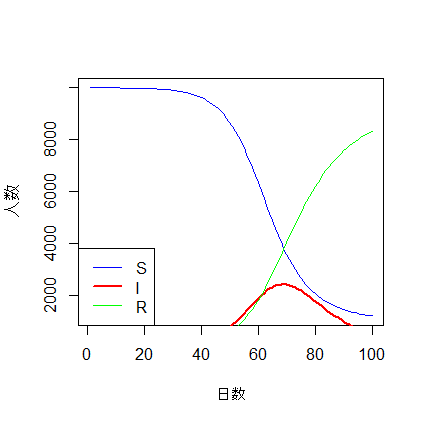
それっぽい曲線が描けた。
初期設定の値は、
S:10000人 + I:1人 + R:0人 = 総人口:N人。
基本再生産数 R0 = 2.5 ・・・ 感染者1人から2.5人に感染
※ 2020年11月の記事 ウイルス再生産
回復率の逆数 γ-1(=1/γ)=Dが分かりにくかったが、平均世代時間と呼ばれる値が使われていた。
感染から回復までの期間つまり感染者が感染力を持っている期間の平均値。
D=10 ・・・ 感染してから他者へ感染させるまでの平均時間10日
感染率 β = R0/(D ・ N)
単位時間あたり単位人口当たりの基本再生産数
R言語のコード(一例)
S <- 10000
I <- 1
R <- 0
N <- S+I+R
R0 <- 2.5
D <- 10.0
B <- R0 / (D*N)
SS <- 1:100
II <- 1:100
RR <- 1:100
for(t in 1:100){
SS[t] <- S
II[t] <- I
RR[t] <- R
dS <- -B*S*I
dI <- B*S*I - (1/D)*I
dR <- (1/D)*I
S <- S+dS
I <- I+dI
R <- R+dR
t <- t +1
}
plot(SS,type="l",col="blue",xlab="日数",ylab="人数")
points(II,type="l",lwd=2,col="red")
points(RR,type="l",col="green")初期値 S、I、R0、Dをいろいろ変えると曲線もいろいろ変わる。
Python
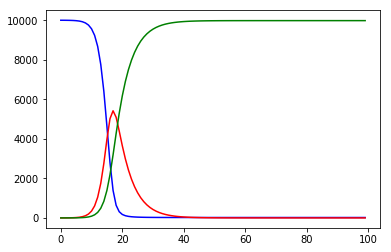
R0を高く、Dを低く変えたら
ピークは高く、早くなった。
この曲線だと未感染者のままい続けられない。
Python(Python 3+Jupyter)のコード(一例)
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
S = 10000
I = 1.0
R = 0
N = S+I+R
D = 5.0
R0 = 5.0
B = R0 / (D*N)
t = 0
SS = list(range(100))
II = list(range(100))
RR = list(range(100))
for t in range(100):
SS[t] = S
II[t] = I
RR[t] = R
dS = -B*S*I
dI = B*S*I - (1/D)*I
dR = (1/D)*I
S = S+dS
I = I+dI
R = R+dR
t += 1
plt.plot(SS,"-",color="blue")
plt.plot(II,"-",color="red")
plt.plot(RR,"-",color="green") 自粛効果、ワクチン効果を考慮したり、
・ 感染者を「発症あり I」と「発症なし(潜伏期) E」に分けたS⇒E ⇒I ⇒R のモデル
・ 回復者が再び感染者になるR ⇒Sのモデル
を試したり……
というのが次のステップだと思うが、
わけ分からない曲線が現れたりしたので、2年近く止まったまま。
数式の理解がその前のステップか……
なんて言っているうちに流行終わりそうだが、
無論終わってくれてよい。
感染症シミュレーションは、ウイルスの感染力が反映されたものだが、
・ ウイルスの病毒性は別
・ 個々の感染防止対策も別
・ 「ロックダウン」を上手く使えない
・ 集団免疫的な理由だけで感染減少していない(と思える)
といった点を考慮すると
街中の「人流」の抑制など行動制限が過剰だなと感じることも正直多かった。経済再生というより「制裁」に感じた人も多かったと思う。
おそらくシミュレーションのうけは良くない。
だが、シミュレーション自体は一理どころか数理ある。
こちらを目の敵にして無意味と断じてしまうのではなく、
「総合的な判断」のほうに無理が生じてしまう点をよくよく考えたほうが建設的であると思う。
参考
- 微分方程式と感染症数理疫学 / 稲葉寿 / 2008 / 数理科学
人口数理モデルの第一人者
他に
感染症の数理モデル / 稲葉寿編著 / 2008 / 培風館
などなど - 感染症の数理モデルと対策 / 鈴木絢子、西浦博 / 2020 / 日本内科学会雑誌
西浦博 = 「8割おじさん」
日本内科学会 … 新型コロナウイルス感染症(COVID-19)関連情報(www.naika.or.jp/activity/covid-19/)の2020年11月24日のページから