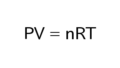熱、エネルギー

　化学反応に伴って出入りする熱は物質ではなくエネルギー。
　燃素（フロギストン）は質量保存の法則によって、
　質量０の物質・熱素（カロリック）はエネルギー保存の法則によって、
過去のモノとなった。
　18世紀後半、産業革命。ワットの蒸気機関が実用化、熱効率（エネルギー効率）向上。
　ただし、熱が熱素（カロリック）ではなくエネルギーであると明確になったのは19世紀前半。
　蒸気機関（熱機関）を“理論的に”考察した最初の人・カルノーも物質かエネルギーか決めかねていた。
　ジュールが羽根車で水を攪拌させて、その仕事（力学的エネルギー）が熱に変換されることを証明、発生した熱量（熱エネルギー）を測定した。

　現在、
　1[cal] ＝ 4.186[J]
　　カロリー　[cal]もジュール　[J]もエネルギーの単位
　　１[cal]は純水１[g]の温度を１[K（ケルビン）]上げるのに必要な熱量（熱エネルギー）

　電力の単位として使われているワット　[W]は仕事率の単位。
　1[W] ＝ 1[J／s]

　馬力も仕事率の単位。

　電力量の単位として使われているワット時　[Wh]、キロワット時　[kWh]は仕事、エネルギーの単位。
　1[Wh] = 1[W] × 3600[s] ＝ 3600[J]
　1[kWh] = 1000[W] × 3600[s] ＝ 3.6×10⁶[J]

エネルギー　Energy

　前回とりあげた理想気体の状態方程式　PV ＝ nRTの左辺PV（圧力×体積）は、
　［N/m²］・［m³］＝ ［N（ニュートン）・m（メートル）］＝ ［J（ジュール）］
なので、エネルギーの次元。
　　※　P ＝ F／S
　　　　PV ＝ F・x　・・・　仕事　W（力学的エネルギー）

　PVがエネルギーの次元ならば、右辺nRT（物質量×気体定数×温度）もエネルギーの次元になるが、
　Rは定数なので、ほとんど温度　Tの式。

　気体の場合、分子個々の運動について考えるのは現実的ではないが、１つの集まりと捉えて全体のエネルギー　＝　内部エネルギー　Uという量で表すことができる。
　理想気体の場合、内部エネルギー　Uは温度　Tのみの関数になる。
　　気体分子運動論
　　単原子分子の場合、U ＝ (3／2)nRT

　なお、熱エネルギー　Qと温度　Tの関係は、
　Q = CT
　　C：熱容量

　　熱容量　大　・・・　温度変化しにくい

エネルギー保存則

　化学のはずが、だんだん物理になっていく。熱化学～熱力学。

　力学的エネルギー保存則は、
　位置エネルギー　＋　運動エネルギー　＝　一定
　　位置エネルギー
　　　mg・h
　　　　mg：重力　[N]
　　　　h：高さ　[m]
　　運動エネルギー
　　　(1/2)mv²
　　　　m：質量　[g]
　　　　v：速度　[m/s]

　　　　1[N] ＝ 1[kg・m/s²]

　　保存（一定）なので、位置エネルギーが減少すれば、その分、運動エネルギーが増大。

　摩擦、空気抵抗を無視した時、保存されるが、
　実際は摩擦、空気抵抗によって力学的エネルギー減少。熱エネルギーへ変換。
　熱エネルギーも考慮すれば、全体のエネルギーは保存される。

　熱力学第１法則はエネルギー保存則。
　Q ＝ W ＋ U
　　Q：熱エネルギー
　　W：外部へ働く仕事　＝　PV
　　U：内部エネルギー

　　外部から加えられる仕事　W’（＞0）の場合（W’＝－W）、
　　　Q + W’ ＝ U